前言
本章节博客是在使用一段时间Dotween后，对于Dotween是如何实现各种不同的缓动类型效果比较好奇。从本片博客会了解线性方程与线性代数之间的关系，以及数学(线性方程)在缓动中的实际应用和数学公式是如何输出显示的。本博客着重于学习数学在插值动画上的运用学习，博客末尾会给出实战的Git地址。
数学
在开始之前，让我们先来了解下如何编写网页版数学公式，然后用于我们的MarkDown中显示。
紧接着我们来回顾和学习了解，线性方程和线性代数各自的概念以及他们之间的关系。
数学公式
考虑到MarkDown或者网页显示数学公式都要有额外的插件支持，所以这里采用独立第三方制作公式显示，然后截图使用图片的形式来显示到MarkDown和网页上。
公式制作
通过搜索了解到LaTeX，是一种基于TeX的排版系统
LateX表达数学公式支持两种方式：
inline mode(is used to write formulas that are part of a text)
inline mode采用以下分隔符:
\( \),$ $or\begin{math} \end{math}
display mode(is used to write expressions that are not part of a text or paragraph, and are therefore put on separate lines.)
由于LateX规则过于庞大，所以这里只是简单的用到什么查什么。
更多更详细的学习参考:
Latex数学公式编写介绍
接下来只是以简单的二元一次方程组为示例，来学习LateX的数学表达结构:
先来看看最终要的效果：
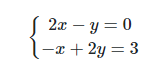
实战：
这简单的二元一次方程，涉及到如下几个概念：
直接上最终LateX代码：
1
2
3
4
5
6
| \usepackage{amsmath}
\begin{align*}
& \left( 2x - y = 0 \right) \\
& \left( -x + 2y = 3 \right)
\end{align*}
|
输出效果:
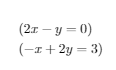
上面没有找到如何输出{符号，忘知道的朋友告知。
上面这种表达方式，我们可以理解成方程组的行表达形式
在线编写LateX网址
上面那个LateX网址是收费的，其次是完全自己写LateX语法符号来编写数学公式。后来发现了更加可视化容易编写数学公式的在线免费网站，有兴趣的可以了解下：
mathcha
只需要按照规则输入符号就能打出想要的数学公式效果。
公式可视化
解决了函数编写输出，那么肯定希望更直观的看到函数的二维坐标系绘图，这里我找到一个在线绘制数学函数的网站：
WolframAlpha
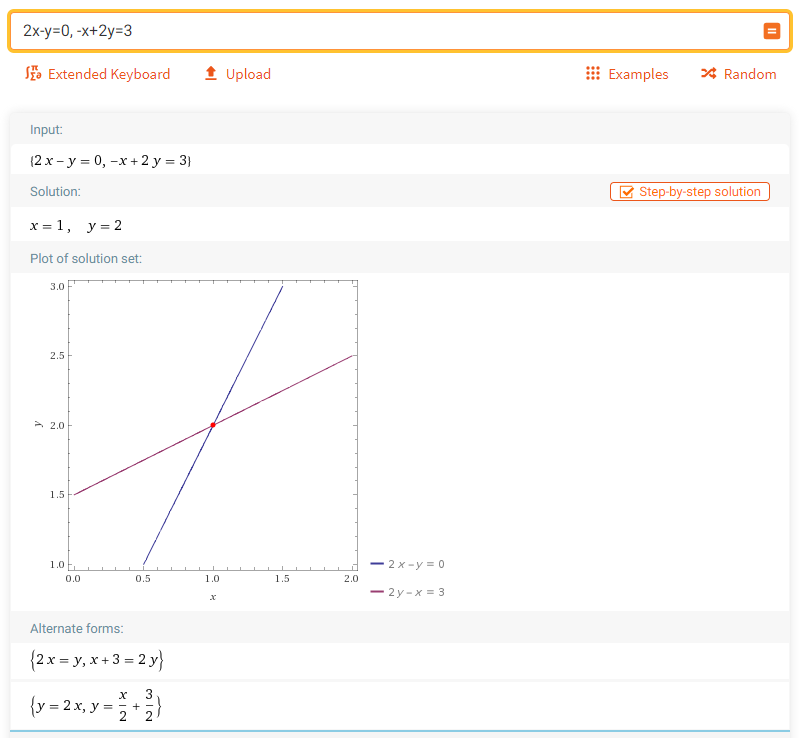
线性方程
线性方程，这个应该是初中学习的知识，参考前面的示例来回顾一下：
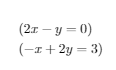
方程组又称联立方程，是两个或两个以上含有多个[未知数]联立得到的[集]。未知数的值称为方程组的[根]，求方程组根的过程称为解方程组。)
这里就不深入探讨了，总之就是解方程组。这里我们更关注的是方程组是如何和线性代数关联上的。
线性代数
线性代数是关于向量空间的一个数学分支。它包括对线、面和子空间的研究，同时也涉及到所有的向量空间的一般性质。)
前面的二元一次方程示例用不同的角度来思考和表达。
以列表达形式如下：
1
2
3
| \begin{equation}
x \binom{2}{1} + y \binom{-1}{-2} = \binom{0}{3}
\end{equation}
|
效果：
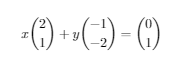
结合二维坐标系：
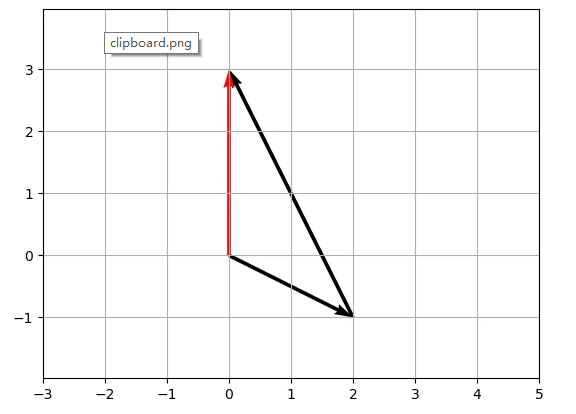
图中是以向量的概念来绘制方程组图像，可以看到矩阵的概念已经呼之欲出了。
以矩阵的概念来表达如下：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
| \qquad \qquad \qquad \qquad \qquad \quad
$\begin{bmatrix}
2 & -1 \\
-1 & 2
\end{bmatrix}$
$\begin{bmatrix}
x \\
y
\end{bmatrix}$
=
$\begin{bmatrix}
0 \\
3
\end{bmatrix}$
|
效果：
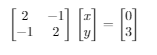
以下截图来源：
可以看出落实到矩阵的概念上，就是对于向量的矩阵变换问题了。向量X通过矩阵A的变换变换到b。
矩阵变换正是线性代数中的一部分。
矩阵可以帮助我们对于复杂的多维函数方程更方便的构造和求解。
更多在线学习参考:
方程组的几何解释
插值
相比前面的数学基础概念，总算进入更有趣的实战环节了。
插值缓动效果是指游戏里一些需要缓慢变化的动画效果(e.g. 移动位置插值，透明度变化插值，颜色变化插值等)。
一般来说在Unity里要实现插值，我们会直接通过类似Update(e.g. Update或Coroutine)的形式去累加时间，然后通过Unity提供的插值函数来获取当前插值的进度值，最终使用这个进度值参与插值运算得出最终插值效果。
所以我们会看到类似以下的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
| using System.Collections;
using UnityEngine;
public class LerpBaseMono : MonoBehaviour {
public float LerpDurationTime = 2.0f;
protected ELerpType mLerpType = ELerpType.None;
void Start () {
DoLerpPrepation();
StartCoroutine(LerpCoroutine());
}
protected virtual void DoLerpPrepation()
{
}
protected IEnumerator LerpCoroutine()
{
var starttime = Time.time;
var endtime = starttime + LerpDurationTime;
while(Time.time < endtime)
{
DoLerp(starttime, endtime, Time.time);
yield return null;
}
DoLerp(starttime, endtime, Time.time);
}
protected virtual void DoLerp(float starttime, float endtime, float currenttime)
{
var t = Mathf.InverseLerp(starttime, endtime, currenttime);
Debug.Log($"开始时间:{starttime}结束时间:{endtime}当前时间:{currenttime}当前缓动值:{t}");
DoRealLerp(t);
}
protected virtual void DoRealLerp(float t)
{
}
}
|
输出如下:
接下来有了缓动的插值t,我们就可以做不同的缓动动画效果了。
上面的代码已经为挂载不同的缓动效果做了设计准备，接下来让我们实现三个简单的缓动效果:
- 位移缓动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
|
public class PositionLerpMono : LerpBaseMono
{
public Vector3 EndPos = Vector3.zero;
protected Vector3 mStartPos;
protected override void DoLerpPrepation()
{
base.DoLerpPrepation();
mLerpType = ELerpType.LerpPosition;
mStartPos = transform.localPosition;
}
protected override void DoRealLerp(float t)
{
transform.localPosition = Vector3.LerpUnclamped(mStartPos, EndPos, t);
}
}
|
- 缩放缓动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
|
public class ScaleLerpMono : LerpBaseMono
{
public Vector3 EndScale = Vector3.one;
protected Vector3 mStartScale;
protected override void DoLerpPrepation()
{
base.DoLerpPrepation();
mLerpType = ELerpType.LerpScale;
mStartScale = transform.localScale;
}
protected override void DoRealLerp(float t)
{
transform.localScale = Vector3.LerpUnclamped(mStartScale, EndScale, t);
}
}
|
- 透明度缓动
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
|
[RequireComponent(typeof(Graphic))]
public class AlphaLerpMono : LerpBaseMono
{
public float EndAlpha = 0.0f;
protected Graphic mGraphicComponent;
protected float mStartAlpha;
protected override void DoLerpPrepation()
{
base.DoLerpPrepation();
mGraphicComponent = GetComponent<Graphic>();
mStartAlpha = mGraphicComponent.color.a;
}
protected override void DoRealLerp(float t)
{
var oldcolor = mGraphicComponent.color;
oldcolor.a = Mathf.Lerp(mStartAlpha, this.EndAlpha, t);
mGraphicComponent.color = oldcolor;
}
}
|
效果如下:
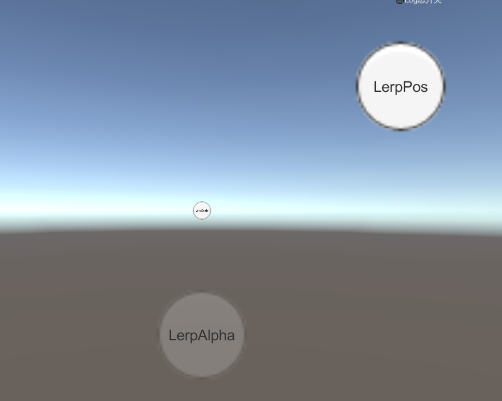
通过上面可以看到我们已经实现了一个简陋版的不同Lerp效果的插值动画。
插值线性方程
接下来就要引入之前提到的线性方程了，从上面可以看出DoRealLerp里的参数t决定了缓动效果的最终进度值，现阶段t的值是通过世间累加然后Lerp插值到0-1的，也就是说是线性的速度。
1
| var t = Mathf.InverseLerp(starttime, endtime, currenttime);
|
这里的线性速度换成线性方程的话，可以理解成y=x
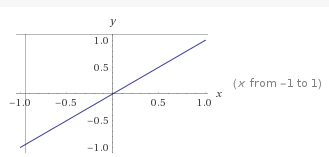
也就是说如果我们把t的变化速度函数修改成其他的线性方程，那就能达到同样的Lerp效果以不同的插值函数来表现。
让我们先通过easings.net来预览下插值函数大概长什么样:
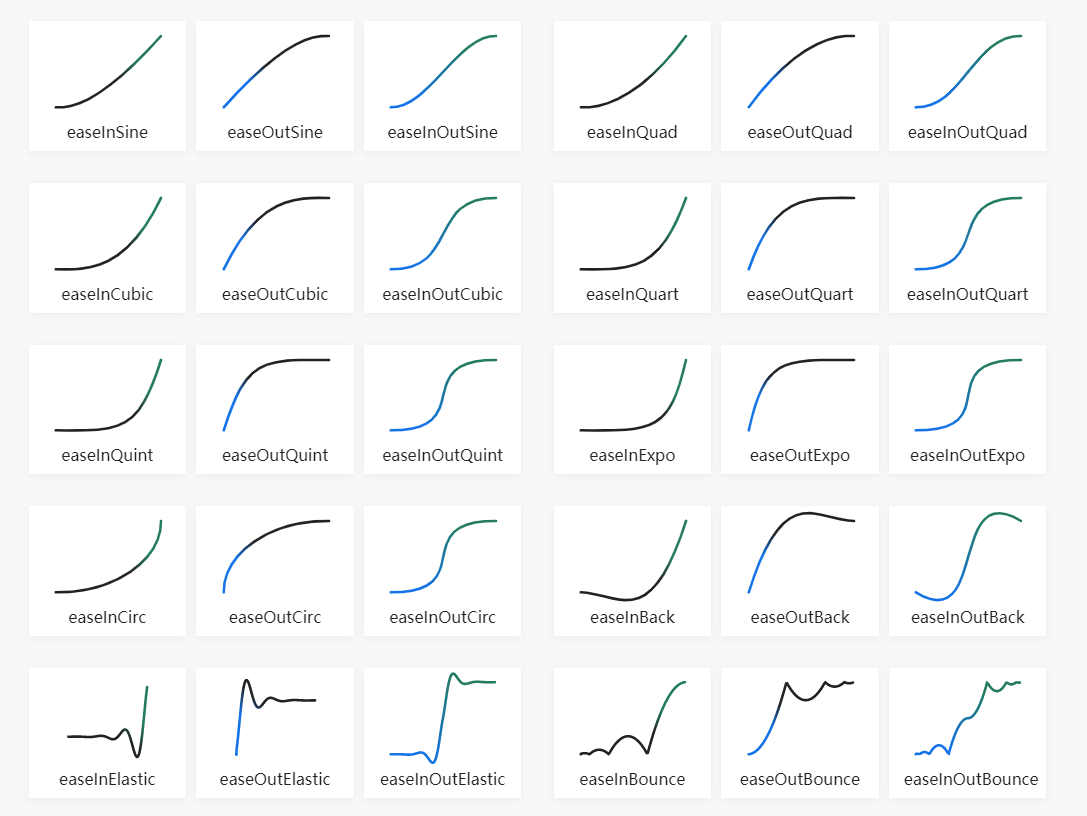
这里核心思想是想替换t的插值计算方式，这里关于插值函数的代码就直接采用Github上现成的了:
EasingFunctions.cs
修改基类代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
|
public class LerpBaseMono : MonoBehaviour {
public float LerpDurationTime = 2.0f;
public EasingFunction.Ease EaseType = EasingFunction.Ease.Linear;
void Start () {
StartCoroutine(LerpCoroutine());
}
protected virtual void DoLerpPrepation()
{
}
protected IEnumerator LerpCoroutine()
{
DoLerpPrepation();
var starttime = Time.time;
var endtime = starttime + LerpDurationTime;
while(Time.time < endtime)
{
DoLerp(starttime, endtime, Time.time);
yield return null;
}
DoLerp(starttime, endtime, Time.time);
}
protected virtual void DoLerp(float starttime, float endtime, float currenttime)
{
var t = Mathf.InverseLerp(starttime, endtime, currenttime);
var easefunc = EasingFunction.GetEasingFunction(EaseType);
t = easefunc(0, 1, t);
DoRealLerp(t);
}
protected virtual void DoRealLerp(float t)
{
}
}
|
这样一来我们就成功的替换了缓动的线性方程，且限定了缓动值t在0-1范围内，实现了不同缓动速度的t。
让我们来看看最终效果:
正如我们预期的那样，同样的终点和持续时间，三个不同缓动类型(线性方程)的移动插值，表现出了不一样的速度变化。
插值组件
上面我们的缓动组件已经雏形已经有了，接下来就是重新好好设计重构以下我们的缓动组件来达到通过挂在缓动组件能快速得到类似Dotween一样的代码效果。
用过Dotween都知道Dotween通过扩展方法的形式和泛型的形式，方便的支持了快速调用动画接口，接下来来看看Dotween几个大的概念设计：
Tweener是单个动画对象的抽象。
Sequence是多个动画Tweener的组合管理抽象。
所以借助于Tweener和Sequence再加上内部插值缓动的Ease的支持，能快速的触发各种缓动方程的动画组合拼接。
这里就不详细讲解Dotween的学习使用了，这里放一张官网Sequence的代码示例来感受一下，Dotween是如何快捷高效的支持多种缓动方程多个动画效果的编写的:
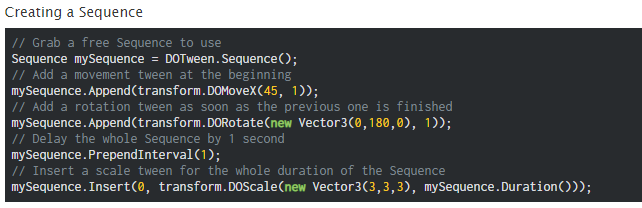
接下来参考Dotween的设计，我将动画组件UML设计如下:
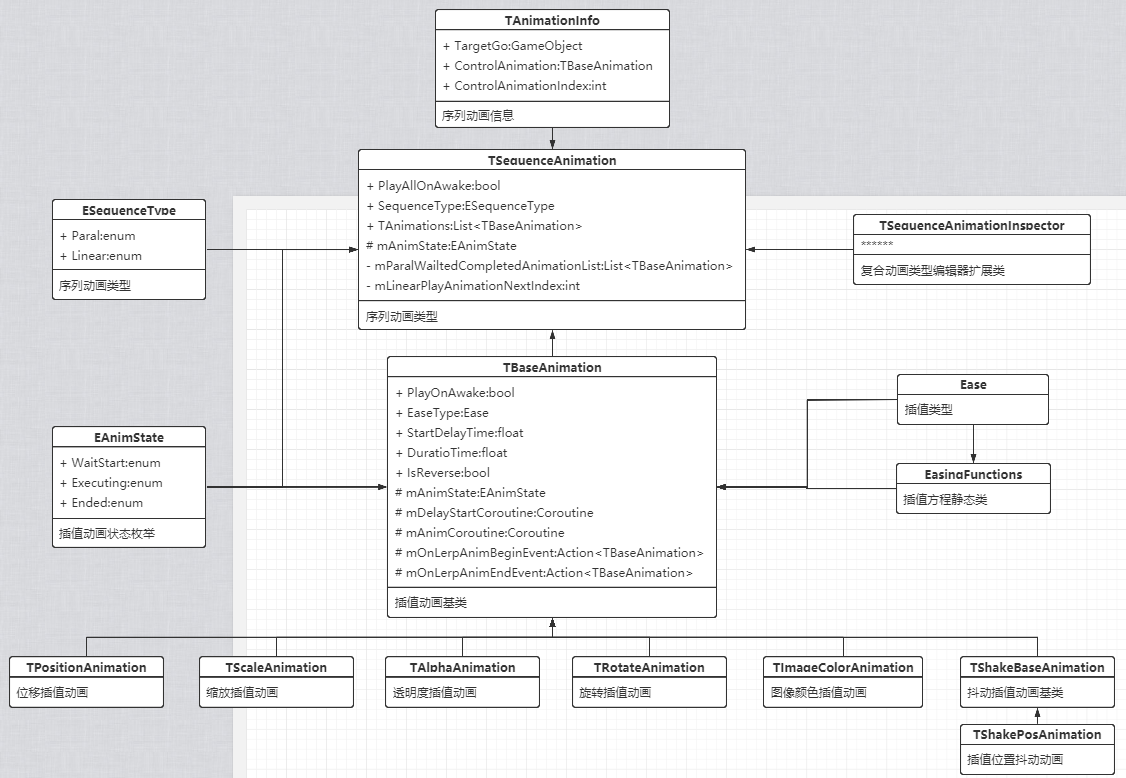
编辑器面板扩展模拟播放:
可以把上面的设计理解成组件版的简陋Dotween:
TBaseAnimation.cs
所有插值动画的基类(抽象网络插值动画的流程以及基础支持),支持是否Awake时自动播放，插值类型，延迟时间，持续时间，循环类型设置等基础设置
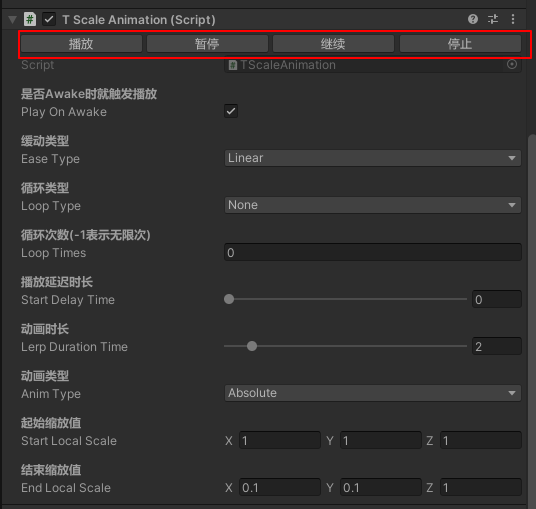
TBaseAnimationEditor.cs
插值动画自定义面板，核心扩展支持了Editor快速模拟播放，暂停，继续，停止按钮功能。
TSequenceAnimation.cs
序列动画抽象,负责像Dotween的Sequence一样管理一系列TBaseAnimation的整体播放效果(比如线性播放和并发播放，目前仅支持单次或无限循环播放两种方式)
TSequenceAnimationEditor.cs
序列动画的自定义面板，核心是通过SerializeObject和SerializeProperty编写支持Undo的自定义序列动画面板，同时支持了Editor快速模拟播放，暂停，继续，停止按钮功能。
EasingFunctions.cs
Git上找的关于不同插值动画类型的核心函数方程定义,把时间插值比列通过不同的函数方程计算出不同的插值系数，从而实现不同的插值方程式的插值动画效果
TPositionAnimation.cs, TScaleAnimation.cs, TAlphaAnimation.cs ……
落实到具体的插值动画类型的实现类
总结
- 通过起始时间，结束时间，当前时间我们可以计算出当前的插值比例。然后通过数学方程将插值比例使用不同的数学方程转换成我们不同插值类型的插值比例从而得到我们想要的不同函数插值效果。
- 组件式的插值动画相比之下没有纯代码(e.g. Dotween)那么高效和可控，但重用性高，方便快速制作简单的程序化动画。
- SerializeObject和SerializeProperty的使用就好比对象和反射属性之间的概念和关系，使用SerializeObject和SerilizeProperty能方便的使用Unity的Undo系统。
Git地址
Ease Component
Reference
Animation & Easing functions in Unity (Tween)
Easing functions
EasingFunctions GitHub
Dotween
DOTween 动画引擎仿写
线性代数)
方程组的几何解释
线性代数与方程的关系（笔记）
LATEX
在线编写LateX网址)
Latex数学公式编写介绍
WolframAlpha
