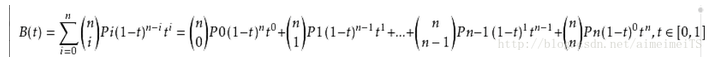文章目錄

1. Introduction
2. 路点编辑和缓动
1. 2.1. Bezier曲线
2. 2.2. 实战
3. 学习总结
4. Github
5. Reference

Introduction

游戏开发过程中，我们希望角色物体按固定路线移动，我们一般需要通过路点编辑器工具去预先编辑好所有路点，然后导出路点数据通过数学运算去移动角色物体。

结合以前学习的数学缓动和UnityEditor知识

本章节通过编写纯Editor的路点编辑器，从实战角度去利用数学缓动和UnityEditor知识实现我们需要的路点编辑器工具，以及基于路点编辑器数据的路线插值缓动系统。

路点编辑和缓动

实现一个工具，首先第一步，我们还是需要理清需求：

纯Editor非运行时路点编辑器。
路点编辑器需要生成可视化编辑对象和路点路线展示(支持纯Editor绘制和LineRenderer组件绘制两种方式)。
路点编辑器要支持指定起始位置和固定位置偏移的路点编辑自动矫正(方便固定单位间隔的路点配置)。
路点编辑器要支持指定路线移动时长，是否循环和是否自动更新朝向等路线缓动模拟设置。
路点编辑器要支持自定义数据导出自定义格式数据。
路点编辑器要支持多种路线类型(e.g. 直线，Bezier，CubicBezier等)。
路线移动支持缓动曲线配置。
路点编辑器要支持纯Editor模拟运行路点移动效果。
路点编辑器编辑完成后的数据要支持运行时使用并模拟路线缓动，同时路线缓动要支持纯运行时构建使用。
实现一个纯Editor的Tile可视化绘制脚本(方便路点编辑位置参考)。

Bezier曲线

我们路点编辑器要支持直线和曲线运动，说到曲线运动，这里就不得不提Bezier曲线。

贝塞尔曲线是电脑图形学中相当重要的参数曲线。

个人理解Bezier曲线的核心原理就是多个点(N阶)之间的同时递归插值0-1比例值得出的一系列最终插值位置

线性Bezier曲线

线性Bezier曲线其实就是我们2个点位置的线性插值，公式如下(P0第一个点，P1第二个点)：

B(t) = P0 + (P1 - P0) * t，t∈[0, 1]

一阶Bezier曲线公式简化后:

B(t) = (1 - t) P0 - t P1，t∈[0, 1]

从公式可以看出，线性Bezier就是2个点位置通过0-1的比例值插值的过程。

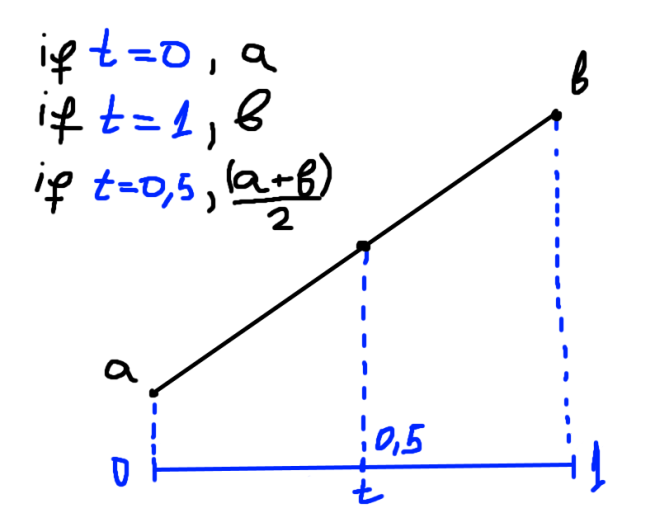
LineBezierIntroduction

二阶Bezier曲线

同理二阶Beizer曲线是由3个顶点位置递归插值而来的，公式如下(P0第一个点，P1第二个点，P2第三个点)：

首先我们先我们先插值P0和P1：

P0P1 = (1 - t) P0 + t P1，t∈[0, 1]

接下来插值P1和P2：

P1P2 = (1 - t) P1 + t P2，t∈[0, 1]

三个点之间的插值完成后，接下来我们还要递归插值三个点插值后的两个点(P0P1和P1P2)：

p0p1p2 = (1 - t) p0p1 + t p1p2，t∈[0, 1]

二阶Bezier曲线公式简化后:

B(t) = (1 - t)² P0 + 2 (1 - t) t P1 + t² * P2，t∈[0, 1]

三阶Bezier曲线

同理三阶Beizer曲线是由3个顶点位置递归插值而来的，公式如下(P0第一个点，P1第二个点，P2第三个点，P3第四个点)：

首先我们先我们先插值P0和P1：

P0P1 = (1 - t) P0 + t P1，t∈[0, 1]

接下来插值P1和P2：

P1P2 = (1 - t) P1 + t P2，t∈[0, 1]

接下来插值P2和P3：

P2P3 = (1 - t) P2 + t P3，t∈[0, 1]

以上插值位置动画如下:

BezierAnimation

P0P1,P1P2,P2P3分别对应动画中的a,b,c三个插值点

四个点之间的插值完成后，接下来我们还要递归插值四个点插值后的三个点(P0P1，P1P2和P2P3)：

插值P0P1和P1P2：

P0P1P2 = (1 - t) P0P1 + t P1P2，t∈[0, 1]

插值P1P2和P2P3：

P1P2P3 = (1 - t) P1P2 + t P2P3，t∈[0, 1]

以上插值位置动画如下:

BezierAnimation2

P0P1P2和P1P2P3分别对应动画中的d和e两个插值点

最后一步，我们接着把P0P1P2和P1P2P3进行插值就能得到3阶Bezier曲线的最终插值位置了:

插值P0P1P2和P1P2P3：

P0P1P2P3 = (1 - t) P0P1P2 + t P1P2P3，t∈[0, 1]

三阶Bezier曲线公式简化后:

B(t) = (1 - t)³ P0 + 3 (1 - t)² t P1 + 3 t² (1 - t) P2 + t³ P3，t∈[0, 1]

以上插值位置动画如下:

BezierAnimation3

N阶Bezier曲线公式参考:

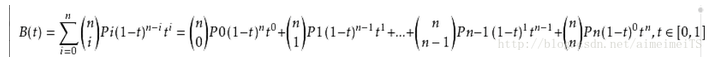
NBezierFormular

N阶Bezier的代码实现请参考:

unity利用高阶贝塞尔曲线进行的轨道移动

由于N阶Bezier的计算复杂度过高，一般来说，路点过多的情况下，我们不会直接采用N阶Bezier曲线进行插值计算，而是采用N个3阶Bezier曲线进行拼接组装成一个N阶Bezier曲线

Catmull-Rom Spline

虽然Bezier已经能实现大部分曲线的需求，但Bezier曲线里移动控制点(无论2阶还是3阶)就会导致整个曲线发生变化，即无法局部控制曲线走向，同时Bezier曲线不能确保通过所有控制点。

Catmull-Rom Spline样条线是一根比较特殊的Bezier曲线，这条Bezier曲线能够保证穿过从控制点的第二个点到控制点的倒数第二点之间的所有点。所以说，Catmull-Rom样条线最少需要4个控制点来进行控制。

Catmull-Rom算法保证两点：

1、点Pi 的一阶导数等于Pi+1 - Pi-1，即点Pi 的切向量和其相邻两点连线的切向量是平行的

2、穿过所有Pi 点。这是与贝塞尔曲线的最大区别，正因为这样的特性，使得Catmull-Rom算法适于用作轨迹线算法。

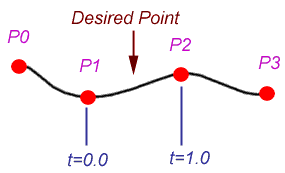
CatmullRomSpline

可以看到Catmull-Rom Spline和三阶Bezier曲线一样需要4个点：

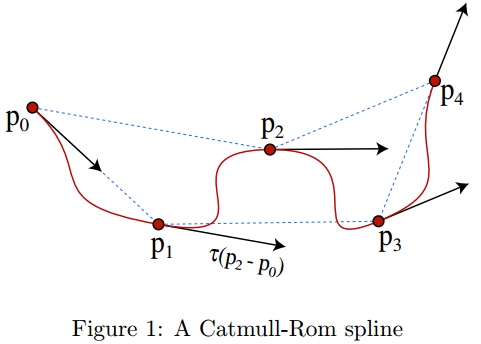
CatmullRomSpline2

P1点的切线和P0P2一致，P2点的切线和P1P3一致。

值得注意的是虽然输入点有4个，但我们t(0-1)最终绘制的是P1到P2和P2到P3这部分

那么如何确保所有的控制点都连接绘制了？

利用Catmull-Rom Spline曲线会通过中间两个控制点且中间两个点经过时的切线与前后两个控制点连线平行，那么我可以可以通过模拟构造一个P(-1)=2P0-P1(确保P(-1)P1和P0切线平行从而确保从P0处切线平行)，利用P(-1)P0P1P2构造一个CatmullRomSpline曲线即可画出P0开始的P0P1的曲线。最后一段曲线同理，构造一个P(N+1)=2P(N)-P(N-1)，然后绘制P(N-2)P(N-1)P(N)P(N+1)即可绘制出P(N-1)P(N)的曲线。

这里直接给出最终推导公式，详细推导过程参考后续其他博主分享：

P = _point = P0 (-0.5ttt + tt – 0.5t) + P1 (1.5ttt - 2.5tt + 1.0) + P2 (-1.5ttt + 2.0tt + 0.5t) + P3 (0.5ttt – 0.5t*t);

详细的推导过程博主并没有完全看懂，这里大家可以参考这位博主的推导分析:

Catmull-Rom插值算法

理解了Bezier曲线和Catmull-Rom Spline样条线原理，接下来让我们进入路点编辑器实战。

实战

接下来针对前面提到的需求，我们一一分析我们应该用什么方案和技术来实现。

需求：

纯Editor非运行时路点编辑器。
路点编辑器需要生成可视化编辑对象和路点路线展示(支持纯Editor绘制和LineRenderer组件绘制两种方式)。
路点编辑器要支持指定起始位置和固定位置偏移的路点编辑自动矫正(方便固定单位间隔的路点配置)。
路点编辑器要支持指定路线移动时长，是否循环和是否自动更新朝向等路线缓动模拟设置。
路点编辑器要支持自定义数据导出自定义格式数据。
路点编辑器要支持多种路线类型(e.g. 直线，Bezier，CubicBezier等)。
路点编辑器要支持纯Editor模拟运行路点移动效果。
路线移动支持缓动曲线配置。
路点编辑器编辑完成后的数据要支持运行时使用并模拟路线缓动，同时路线缓动要支持纯运行时构建使用。
路线移动支持缓动曲线配置。
实现一个纯Editor的Tile可视化绘制脚本(方便路点编辑位置参考)。

实现思路：

结合自定义Inspector面板(继承Editor)定义的方式实现纯Editor配置和操作
利用Gizmos(Monobehaviour:OnDrawGizmos())，Handles(Editor.OnSceneGUI())和自定义Inspector(Editor)面板编辑操作实现可视化编辑对象生成和展示。LineRenderer通过挂在指定LinRenderer组件将路点细分的点通过LineRenderer:SetPositions()设置显示。
利用自定义Inspector面板支持起始位置和路点间隔配置，然后通过配置数据进行路点位置矫正操作。
自定义Inspecotr面板支持配置即可。
同上，自定义Inspector面板支持操作分析路点数据进行导出即可。
利用Bezier曲线知识，实现不同路线类型(e.g. 直线，Bezier，CubicBezier等)。
利用InitializeOnLoad，ExecuteInEditMode和InitializeOnLoadMethod标签加EditorApplication.update实现纯Editor初始化和注入Update更新实现纯Editor模拟路点移动效果。
利用缓动曲线去重新计算插值t(0-1)的值作为插值比例即可。
实现一套超级简陋版DoTween支持运行时路线缓动模拟即可(见TPathTweener和TPathTweenerManager)。
利用Gizmos的自定义Mesh绘制+自定义Inspector面板实现Tile网格自定义配置绘制。

核心思路和技术实现方案都在上面介绍了，这里就不一一介绍代码实现了，这里只放关于Bezier曲线插值相关的代码，让我们直接实战看效果，需要源码的直接在文章末尾Github链接去取即可。

BezierUtilities.cs(Bezier曲线插值相关)

using System;
using System.Collections;
using System.Collections.Generic;
using UnityEngine;

/// <summary>
/// BezierUtilities.cs
/// Bezier静态工具类
/// </summary>
public static class BezierUtilities
{
    // Note：
    // 1. 高阶Bezier曲线计算复杂，推荐用N个3阶Bezier曲线模拟

    /// <summary>
    /// 根据t(0-1)计算一阶Bezier曲线上面对应的点
    /// </summary>
    /// <param name="p0">第一个点</param>
    /// <param name="p1">第二个点</param>
    /// <param name="t">插值(0-1)</param>
    /// <returns></returns>
    public static Vector3 CaculateLinerPoint(Vector3 p0, Vector3 p1, float t)
    {
        t = Mathf.Clamp01(t);
        // 原始公式:
        /*
        return (1 - t) * p0 + t * p1;
        */
        return (1 - t) * p0 + t * p1;
    }

    /// <summary>
    /// 根据t(0-1)计算二阶贝塞尔曲线上面对应的点
    /// </summary>
    /// <param name="p0">第一个点</param>
    /// <param name="p1">第二个点</param>
    /// <param name="p2">第三个点</param>
    /// <param name="t">插值(0-1)</param>
    /// <returns></returns>
    public static Vector3 CaculateBezierPoint(Vector3 p0, Vector3 p1, Vector3 p2, float t)
    {
        t = Mathf.Clamp01(t);
        // 原始公式:
        /*
        var p0p1 = (1 - t) * p0 + t * p1;
        var p1p2 = (1 - t) * p1 + t * p2;
        return (1 - t) * p0p1 + t * p1p2;
        */
        // 简化运算:
        var u = 1 - t;
        var tt = t * t;
        var uu = u * u;
        return uu * p0 + 2 * u * t * p1 + tt * p2;
    }

    /// <summary>
    /// 根据t(0-1)计算三阶贝塞尔曲线上面对应的点
    /// </summary>
    /// <param name="p0">第一个点</param>
    /// <param name="p1">第二个点</param>
    /// <param name="p2">第三个点</param>
    /// <param name="p3">第四个点</param>
    /// <param name="t">插值(0-1)</param>
    /// <returns></returns>
    public static Vector3 CaculateCubicBezierPoint(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
    {
        t = Mathf.Clamp01(t);
        // 原始公式:
        /*
        var p0p1 = (1 - t) * p0 + t * p1;
        var p1p2 = (1 - t) * p1 + t * p2;
        var p2p3 = (1 - t) * p2 + t * p3;
        var p0p1p2 = (1 - t) * p0p1 + t * p1p2;
        var p1p2p3 = (1 - t) * p1p2 + t * p2p3;
        return (1 - t) * p0p1p2 + t * p1p2p3;
        */
        // 简化运算:
        var u = 1 - t;
        var tt = t * t;
        var uu = u * u;
        var ttt = tt * t;
        var uuu = uu * u;
        return uuu * p0 + 3 * uu * t * p1 + 3 * tt * u * p2 + ttt * p3;
    }

    /// <summary>
    /// 根据t(0-1)计算Cutmull-Roll Spline曲线上面对应的点
    /// </summary>
    /// <param name="p0">第一个点</param>
    /// <param name="p1">第二个点</param>
    /// <param name="p2">第三个点</param>
    /// <param name="p3">第四个点</param>
    /// <param name="t">插值(0-1)</param>
    /// <returns></returns>
    public static Vector3 CaculateCRSplinePoint(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)
    {
        t = Mathf.Clamp01(t);
        // 原始公式:
        /*
         Output_point = (-0.5*t*t*t + t*t – 0.5*t) * p0 +
		                (1.5*t*t*t - 2.5*t*t + 1.0) * p1 +
		                (-1.5*t*t*t + 2.0*t*t + 0.5*t) * p2 +
		                (0.5*t*t*t – 0.5*t*t) * p3;
        */
        // 简化运算:
        var tt = t * t;
        var ttt = tt * t;
        return (-0.5f * ttt + tt - 0.5f * t) * p0 +
               (1.5f * ttt - 2.5f * tt + 1) * p1 +
               (-1.5f * ttt + 2 * tt + 0.5f * t) * p2 +
               (0.5f * ttt - 0.5f * tt) * p3;
    }

    /// <summary>
    /// 获取存储的一阶Bezier曲线细分顶点的数组
    /// </summary>
    /// <param name="p0">第一个点</param>
    /// <param name="p1">第二个点</param>
    /// <param name="segmentNum">细分段数</param>
    /// <returns>存储贝塞尔曲线点的数组</returns>
    public static Vector3[] GetLinerList(Vector3 p0, Vector3 p1, int segmentNum)
    {
        segmentNum = Mathf.Clamp(segmentNum, 1, Int32.MaxValue);
        var pathPointNum = segmentNum + 1;
        Vector3[] path = new Vector3[pathPointNum];
        for (int i = 0; i < pathPointNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pathPoint = CaculateLinerPoint(p0, p1, t);
            path[i] = pathPoint;
        }
        return path;
    }

    /// <summary>
    /// 获取存储的二次贝塞尔曲线细分顶点的数组
    /// </summary>
    /// <param name="p0">起始点</param>
    /// <param name="p1">控制点</param>
    /// <param name="p2">目标点</param>
    /// <param name="segmentNum">细分段数</param>
    /// <returns>存储贝塞尔曲线点的数组</returns>
    public static Vector3[] GetBeizerList(Vector3 p0, Vector3 p1, Vector3 p2, int segmentNum)
    {
        segmentNum = Mathf.Clamp(segmentNum, 1, Int32.MaxValue);
        var pathPointNum = segmentNum + 1;
        Vector3[] path = new Vector3[pathPointNum];
        for (int i = 0; i < pathPointNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pathPoint = CaculateBezierPoint(p0, p1, p2, t);
            path[i] = pathPoint;
        }
        return path;
    }

    /// <summary>
    /// 获取存储的三次贝塞尔曲线细分顶点的数组
    /// </summary>
    /// <param name="p0">起始点</param>
    /// <param name="p1">控制点1</param>
    /// <param name="p2">控制点2</param>
    /// <param name="p3">目标点</param>
    /// <param name="segmentNum">细分段数</param>
    /// <returns>存储贝塞尔曲线点的数组</returns>
    public static Vector3[] GetCubicBeizerList(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, int segmentNum)
    {
        segmentNum = Mathf.Clamp(segmentNum, 1, Int32.MaxValue);
        var pathPointNum = segmentNum + 1;
        Vector3[] path = new Vector3[pathPointNum];
        for (int i = 0; i < pathPointNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pathPoint = CaculateCubicBezierPoint(p0, p1, p2, p3, t);
            path[i] = pathPoint;
        }
        return path;
    }

    /// <summary>
    /// 获取存储的Cutmull-Rom Spline曲线细分顶点的数组
    /// </summary>
    /// <param name="p0">起始点</param>
    /// <param name="p1">控制点1</param>
    /// <param name="p2">控制点2</param>
    /// <param name="p3">目标点</param>
    /// <param name="segmentNum">细分段数</param>
    /// <returns>存储Cutmull-Rom Spline曲线点的数组</returns>
    public static Vector3[] GetCRSplineList(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, int segmentNum)
    {
        segmentNum = Mathf.Clamp(segmentNum, 1, Int32.MaxValue);
        var pathPointNum = segmentNum + 1;
        Vector3[] path = new Vector3[pathPointNum];
        for (int i = 0; i < pathPointNum; i++)
        {
            float t = i / (float)segmentNum;
            Vector3 pathPoint = CaculateCRSplinePoint(p0, p1, p2, p3, t);
            path[i] = pathPoint;
        }
        return path;
    }
}

TPath.cs(M个点换算成P个N阶Bezier曲线插值)

/// <summary>
/// 获取线性路线指定比例路点位置
/// </summary>
/// <param name="t"></param>
/// <returns></returns>
private Vector3 GetLinerPoinAt(float t)
{
    var pointNum = CaculatePathPointList.Count;
    var maxPointIndex = pointNum - 1;
    TSegment currentUnderSegment;
    float currentUnderSegmentPercent;
    GetRadioSegmentAndPercent(t, out currentUnderSegment, out currentUnderSegmentPercent);
    if(currentUnderSegment == null)
    {
        return Vector3.zero;
    }
    var firstPointIndex = currentUnderSegment.StartPointIndex;
    var secondPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 1, 0, maxPointIndex);
    return BezierUtilities.CaculateLinerPoint(CaculatePathPointList[firstPointIndex], CaculatePathPointList[secondPointIndex], currentUnderSegmentPercent);
}

/// <summary>
/// 获取二阶贝塞尔路线指定比例路点位置
/// </summary>
/// <param name="t"></param>
/// <returns></returns>
private Vector3 GetBezierPointAt(float t)
{
    var pointNum = CaculatePathPointList.Count;
    var maxPointIndex = pointNum - 1;
    TSegment currentUnderSegment;
    float currentUnderSegmentPercent;
    GetRadioSegmentAndPercent(t, out currentUnderSegment, out currentUnderSegmentPercent);
    if (currentUnderSegment == null)
    {
        return Vector3.zero;
    }
    var firstPointIndex = currentUnderSegment.StartPointIndex;
    var secondPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 1, 0, maxPointIndex);
    var thirdPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 2, 0, maxPointIndex);
    return BezierUtilities.CaculateBezierPoint(CaculatePathPointList[firstPointIndex],
                                               CaculatePathPointList[secondPointIndex],
                                               CaculatePathPointList[thirdPointIndex],
                                               currentUnderSegmentPercent);
}

/// <summary>
/// 获取三阶贝塞尔路线指定比例路点位置
/// </summary>
/// <param name="t"></param>
/// <returns></returns>
private Vector3 GetCubicBezierPointAt(float t)
{
    var pointNum = CaculatePathPointList.Count;
    var maxPointIndex = pointNum - 1;
    TSegment currentUnderSegment;
    float currentUnderSegmentPercent;
    GetRadioSegmentAndPercent(t, out currentUnderSegment, out currentUnderSegmentPercent);
    if (currentUnderSegment == null)
    {
        return Vector3.zero;
    }
    var firstPointIndex = currentUnderSegment.StartPointIndex;
    var secondPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 1, 0, maxPointIndex);
    var thirdPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 2, 0, maxPointIndex);
    var fourthPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 3, 0, maxPointIndex);
    return BezierUtilities.CaculateCubicBezierPoint(CaculatePathPointList[firstPointIndex],
                                                    CaculatePathPointList[secondPointIndex],
                                                    CaculatePathPointList[thirdPointIndex],
                                                    CaculatePathPointList[fourthPointIndex],
                                                    currentUnderSegmentPercent);
}

/// <summary>
/// 获取Cutmull-Roll Spline路线指定比例路点位置
/// </summary>
/// <param name="t"></param>
/// <returns></returns>
private Vector3 GetCRSplinePointAt(float t)
{
    var pointNum = CaculatePathPointList.Count;
    var maxPointIndex = pointNum - 1;
    TSegment currentUnderSegment;
    float currentUnderSegmentPercent;
    GetRadioSegmentAndPercent(t, out currentUnderSegment, out currentUnderSegmentPercent);
    if (currentUnderSegment == null)
    {
        return Vector3.zero;
    }
    var firstPointIndex = currentUnderSegment.StartPointIndex;
    var secondPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 1, 0, maxPointIndex);
    var thirdPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 2, 0, maxPointIndex);
    var fourthPointIndex = Mathf.Clamp(currentUnderSegment.StartPointIndex + 3, 0, maxPointIndex);
    return BezierUtilities.CaculateCRSplinePoint(CaculatePathPointList[firstPointIndex],
                                                 CaculatePathPointList[secondPointIndex],
                                                 CaculatePathPointList[thirdPointIndex],
                                                 CaculatePathPointList[fourthPointIndex],
                                                 currentUnderSegmentPercent);
}

/// <summary>
/// 获取指定比例路点所处分段和分段所占比例
/// </summary>
/// <param name="t"></param>
/// <param name="segment"></param>
/// <param name="segmentPercent"></param>
private void GetRadioSegmentAndPercent(float t, out TSegment segment, out float segmentPercent)
{
    var pointNum = PathPointList.Count;
    if (pointNum == 0)
    {
        segment = null;
        segmentPercent = 0f;
        return;
    }
    else if (pointNum == 1)
    {
        segment = SegmentList[0];
        segmentPercent = 1f;
        return;
    }
    t = Mathf.Clamp01(t);
    // 缓动公式对路线插值的影响
    var easeFunc = EasingFunction.GetEasingFunction(Ease);
    t = easeFunc(0, 1, t);
    var distance = t * Length;
    segment = SegmentList[0];
    for (int i = 0, length = SegmentList.Count - 1; i < length; i++)
    {
        distance -= SegmentList[i].Length;
        segment = SegmentList[i];
        if (distance < 0)
        {
            break;
        }
    }
    segmentPercent = (segment.Length + distance) / segment.Length;
}

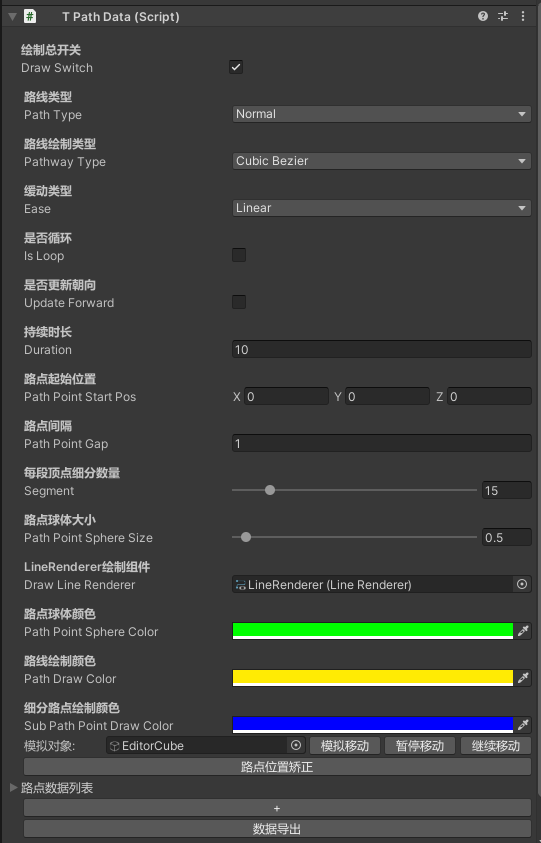
自定义路点数据编辑面板：

CustomPathDataInspector

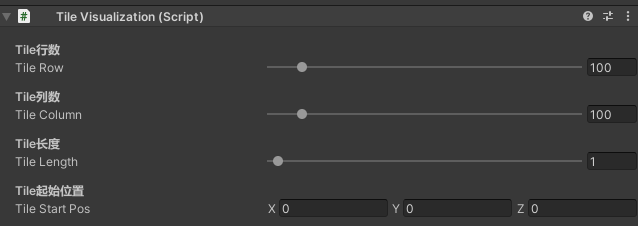
自定义Tile绘制配置面板:

CustomTileInspector

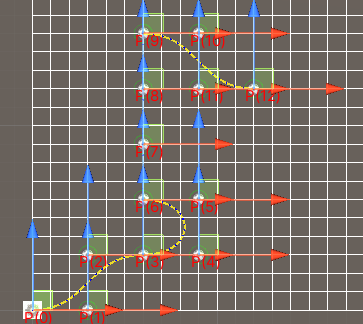
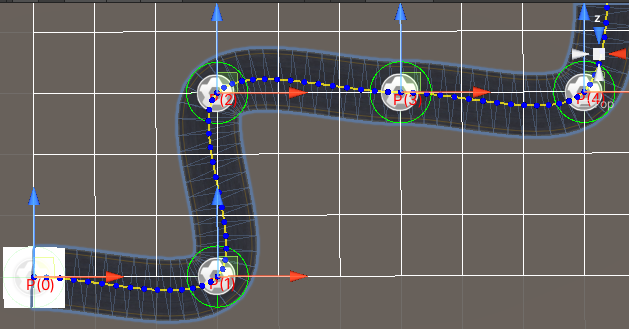
可视化路点路线展示:

CubicBezierDraw

自定义路线数据导出：

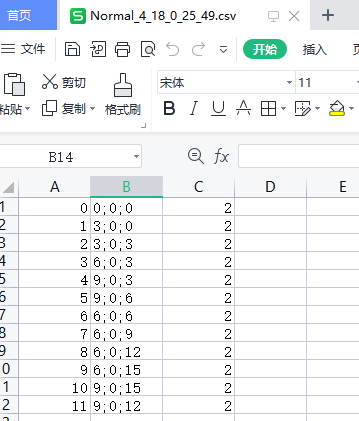
CustomPathDataExport

LineRenderer可视化展示：

CutmullRomSplineDraw

Ease插值类型：

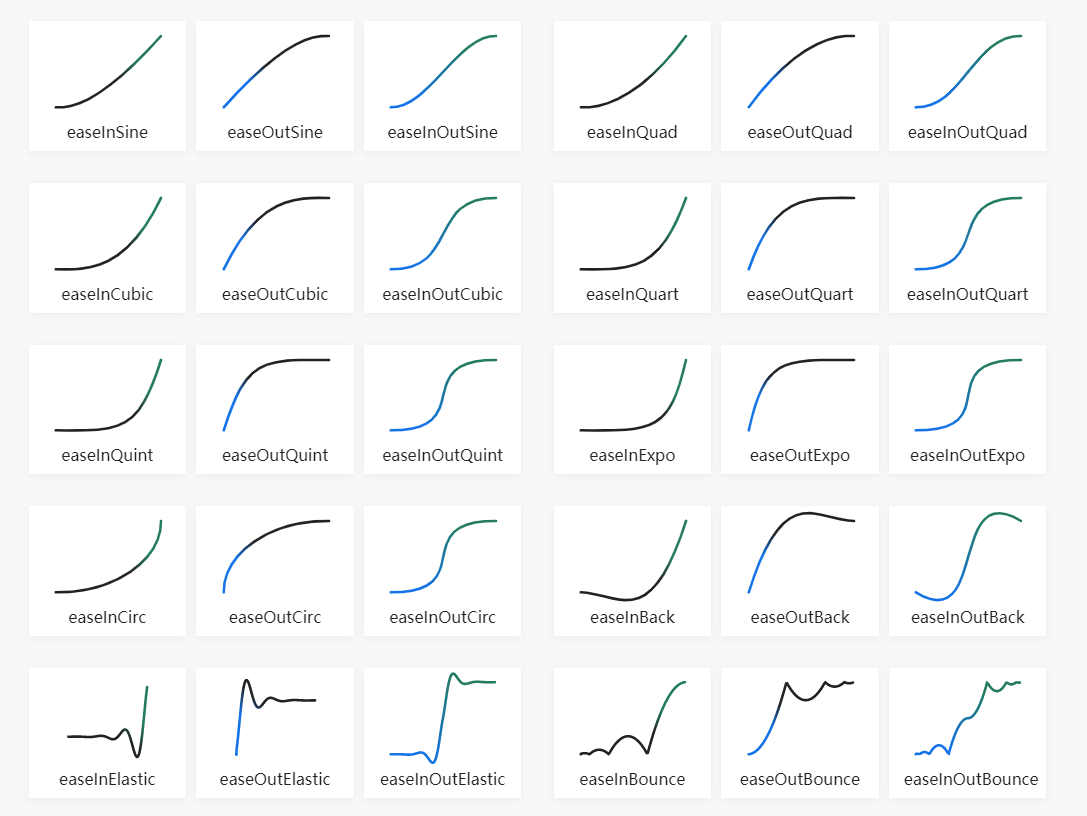
$EaseLerpFunction$

M个点的N个3阶Bezier插值计算思路如下：

N个3阶Bezier曲线的组合插值是通过将M个点分成N段3阶Bezier，计算出总长度且每段Bezier存储起始点索引和Bezier类型(影响当前Bezier的采样点数)和路段长度
当我们要计算一个插值比例t(0-1)进度插值计算时，首先根据总距离和进度映射计算出在哪一段Bezier路段
映射计算到对应3阶Bezier段后，再进行单个3阶Bezier曲线比例插值从而得到我们M个点的插值比例t(0-1)的最终插值位置

Cutmull-Rom Spline曲线经过首尾两个控制点思路：

利用Catmull-Rom Spline曲线会通过中间两个控制点且中间两个点经过时的切线与前后两个控制点连线平行，那么我可以可以通过模拟构造一个P(-1)=2P0-P1(确保P(-1)P1和P0切线平行从而确保从P0处切线平行)，利用P(-1)P0P1P2构造一个CatmullRomSpline曲线即可画出P0开始的P0P1的曲线。最后一段曲线同理，构造一个P(N+1)=2P(N)-P(N-1)，然后绘制P(N-2)P(N-1)P(N)P(N+1)即可绘制出P(N-1)P(N)的曲线。

TODO:

将运行时使用TPathTweenerManager运动的曲线支持可配置化可视化绘制

学习总结

Bezier曲线是一个N个点之间递归插值计算的过程
复杂的很多点路线插值一般不会采用N阶Bezier曲线插值而是采用换算成N个3阶Bezier曲线插值的方式降低计算复杂度
Catmull-Rom Spline确保通过首尾控制点是通过插入头尾两个虚拟点的方式实现的。
缓动结合Bezier曲线的使用主要体现在最后一步插值时对t值的运算替换上
纯Editor模拟更新驱动需要InitializeOnLoad，ExecuteInEditMode和InitializeOnLoadMethod标签加EditorApplication.update实现即使代码编译后也能正确注入和取消EditorApplication.update的流程
LineRenerer默认useWorldSpace为true，表示设置的SetPositions是世界坐标。
LineRenderer有两种朝向显示模式Alignment.View和Alignment.TransformZ，前者是类似BillBoard朝向摄像机，后者是朝向Z轴，一般纯3D路线个人觉得应该是后者加上旋转的方式。
LineRenderer的纹理渲染(Texture Mode)方式有四种，Stretch(使用单次纹理拉伸铺满的方式)，Tile(重复显示，渲染里Tile的概念，基于世界单位长度细分，使用Material.SetTextureScale来设置重复多少次纹理填充)，DistributePerSegment(好像是每个顶点间映射一次纹理，默认假设顶点间间距已经平均好了)，RepeatPerSegment(重复显示纹理，使用Material.SetTextureScale来设置重复多少次纹理填充)。
LineRenderer修改Width后如果细分的点不够多，可能出现即使连接的是直线也在拐角处显示有问题，需要细分更多的点来解决此问题。