数学知识

文章目錄

1. 1. Introduction
2. 2. 3D数学
3. 3. 坐标系
   1. 3.1. 多坐标系
   2. 3.2. 实战
4. 4. 向量
   1. 4.1. 数学定义
   2. 4.2. 几何定义
      1. 4.2.1. 点乘
      2. 4.2.2. 叉乘
      3. 4.2.3. 运用
5. 5. 矩阵
6. 6. 欧拉角与四元数
7. 7. 几何检测
8. 8. 可见性检测
9. 9. 数学概念
10. 10. 学习总结
11. 11. Github
12. 12. Reference

Introduction

Unity游戏开发过程中我需要掌握一些常规的数学知识(比如线性代数)，游戏开发接触的比较多的就是向量和矩阵，本章节用于记录和学习数学相关的知识，好让自己对于平时用到的数学知识有一个归纳和深入的学习总结，避免每次都是久了不用就忘。

推荐书籍:

《3D数学基础:图形与游戏开发》

此书记讲到了游戏开发中需要用到的大部分数学基础知识，以前看这个书的时候是为了学习而学习，没有深入实战，而今天重拾此书，一边实战(结合Unity)一边记录的方式，深入学习游戏开发的数学基础知识，避免出现久了不用就忘的情况，也方便以后温故而知新。

Note:

1. 为了减少重复的代码展示，后续相同代码展示会采用*代替

3D数学

什么是3D数学？

3D数学是一门和计算几何相关的学科，计算几何则是研究用数值方法解决几何问题的学科

坐标系

笛卡尔坐标系在数学中是一种正交坐标系，由法国数学家勒内·笛卡尔引入而得名。二维的直角坐标系是由两条相互垂直、相交于原点的数线构成的。在平面内，任何一点的坐标是根据数轴上对应的点的坐标设定的。在平面内，任何一点与坐标的对应关系，类似于数轴上点与坐标的对应关系。

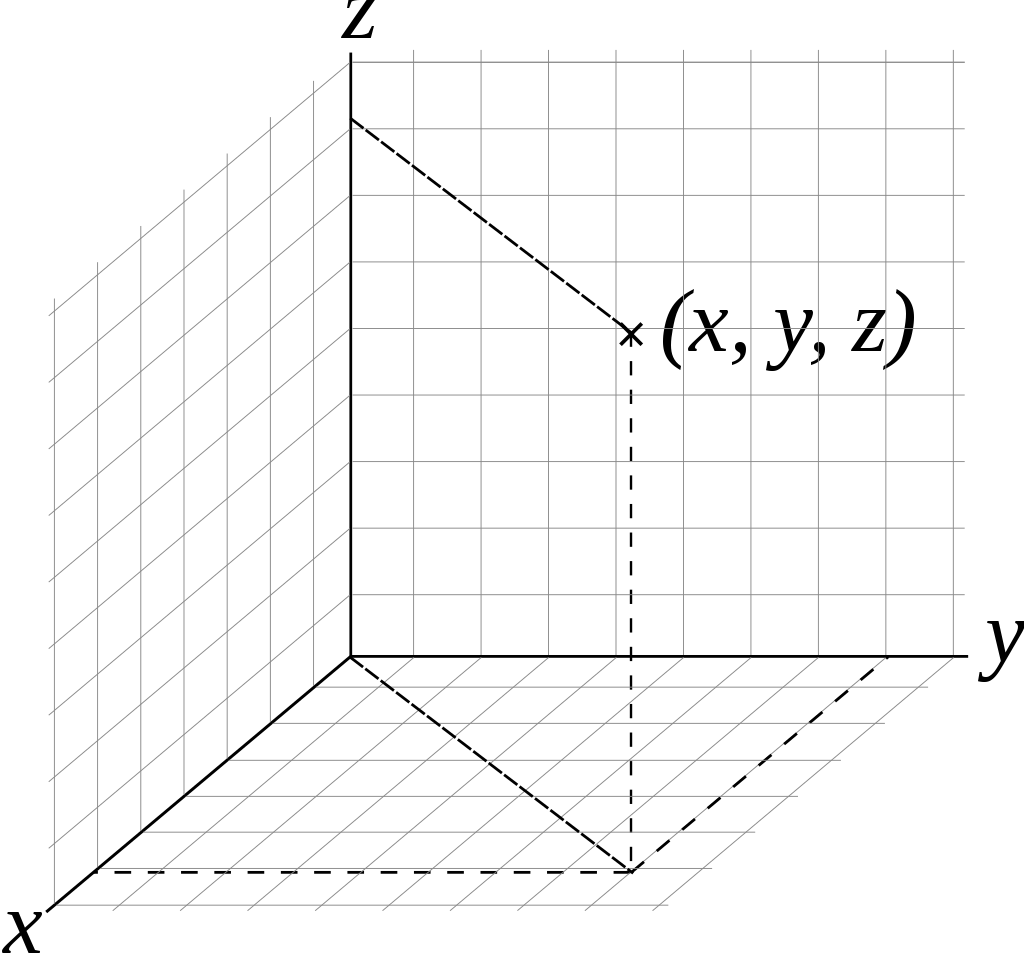
笛卡尔坐标系就是我们以前学习平面几何时学习的坐标系，通过笛卡尔坐标系，我们可以通过x,y,z定义1D,2D或3D等空间的点。

坐标系从大的类型上来分分为两类:

1. 左手坐标系
2. 右手坐标系

如何区分左手还是右手坐标系了？

通过将大拇指指向Z轴正方向，如果其余四指握起是从X轴往Y轴那么就是左手坐标系，反之则是右手坐标系

Note:

1. 大拇指指向X轴，食指指向Y轴，中指指向Z轴
2. Unity是左手坐标系
3. OpenGL是右手坐标系

多坐标系

坐标系不止一种，使用多种坐标系的原因是某些信息只能在特定的上下文环境中获得

比如以前学习OpenGL的时候，就了解到一个三角形要想渲染到屏幕上，需要经历MVP的矩阵变换。

M — Model -> World(模型坐标系到世界坐标系)

变换目的:3D模型是基于自身的坐标系存储的。计算模型各顶点在世界空间的位置，以便将模型摆放到世界空间中。

这里的世界坐标系，就是Unity里我们访问Transform.position时访问到的世界坐标所处的坐标系。

而物体坐标系是相对物体自身而言的坐标系，通过勾选Local，我们可以看到物体自身的坐标系:

通过Model -> World我们就得到了物体在世界坐标系里的位置表达信息。

V — World -> View(世界坐标系到相机坐标系)

变换目的:计算物体对相机的相对位置，以便进行后续变换

P — View -> Projection(摄像机坐标系到投影坐标系)

因为摄像机的投影方式有多种(比如透视投影和正交投影)，所以从摄像机坐标系到投影坐标系也存在着不同的计算方式。

详情参考以前的学习记录:

Coordinate Transformations & Perspective Projection

后续我们学习矩阵概念的时候再深入理解，核心就是通过矩阵执行坐标系转换。

Note:

1. 矩阵变换是由M = S(scale) × R(rotation) × T(translation)组成，且不满足交换律，因为S和R都是针对坐标系原点进行的，一旦先执行T，那么相对于坐标系原点的位置就会有所变化，这之后再做S和R就会出现不一样的表现。

实战

接下来通过使用Unity来更深入的理解坐标系变化:

/* * Description:             CoordinateStudy.cs * Author:                  TONYTANG * Create Date:             2022/03/11 */
 * Description:             CoordinateStudy.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/11
 */

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;

/// <summary>
/// CoordinateStudy.cs
/// 坐标系学习
/// </summary>
public class CoordinateStudy : MonoBehaviour
{
    /// <summary>
    /// 提示文本
    /// </summary>
    [Header("提示文本")]
    public Text TipTxt;

    /// <summary>
    /// Cube1
    /// </summary>
    [Header("Cube1")]
    public GameObject Cube1;

    /// <summary>
    /// Cube2
    /// </summary>
    [Header("Cube2")]
    public GameObject Cube2;

    private void Start()    {
    
        var cube1RelativeCube2Pos = Cube2.transform.InverseTransformPoint(Cube1.transform.position);
        var cube2RelativeCube1Pos = Cube1.transform.InverseTransformPoint(Cube2.transform.position);
        TipTxt.text = $"红色表示Cube1,绿色表示Cube2\n" +
                        $"Cube1世界坐标:{Cube1.transform.position.ToString()} 旋转角度:{Cube1.transform.eulerAngles.ToString()}\n" +
                        $"Cube2世界坐标系:{Cube2.transform.position.ToString()} 旋转角度:{Cube2.transform.eulerAngles.ToString()}\n" +
                        $"Cube1相对Cube2的坐标为:{cube1RelativeCube2Pos.ToString()}\n" +
                        $"Cube2相对Cube1的坐标为:{cube2RelativeCube1Pos.ToString()}";
    }
}

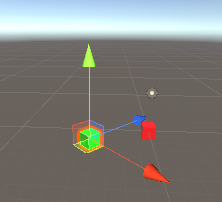
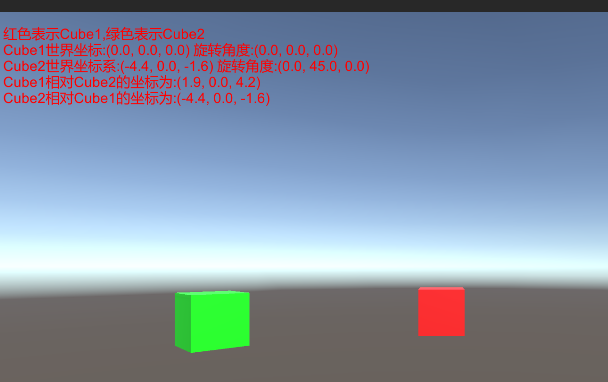
可以看到我通过调用transform.InverseTransformPoint()接口实现了将物体世界坐标转换到另一个物体的局部坐标的转换。因为Cube1在坐标原点且没有旋转，所以Cube2在Cube1物体坐标系里的位置也就是Cube2的世界坐标系位置。而Cube2因为有旋转，所以Cube1在Cube2物体坐标系的位置就需要根据Cube2的本地坐标系来计算了。

考虑到世界坐标系到视口坐标系转换后平时用不上，所以这里就不可视化结果了，通过Camera.WorldToViewportPoint()接口可以把世界坐标转换到摄像机视口坐标。同理Camera.WorldToScreenPoint()可以把世界坐标转换到屏幕坐标，这个接口相对而言更常用些(比如3D映射2D UI显示的时候)。

Note:

1. 如果想查看物体本地坐标系和世界坐标系的转换矩阵，Unity里可以通过Transform.localToWorldMatrix()和Transform.worldToLocalMatrix()接口拿到变换的矩阵

向量

向量有两种不同但相关相关的意义，一种是纯抽象的数学意义，另一种是几何意义。

数学定义

向量就是一个数字列表，对程序员而言则是另一种类似的概念—数组

行向量(1行3列):

[1, 2, 3]

列向量(一列三行):

[ 1 ]

[ 2 ]

[ 3 ]

向量中的数表达了每个维度上的有向位移。比如上面的向量在坐标系里表达的是相对[0,0,0]原点的X,Y,Z轴分别位移1,2,3

Note:

1. 注意区分向量和标量，标量是平时用的数字的技术称谓

几何定义

向量是有大小和方向的线段。

向量的大小就是向量的长度(模)。向量有非负的长度。

向量的方向描述了空间中向量的指向。

向量模 = Sqrt(VX VX + VY VY + VZ * VZ)

向量里有一个比较重要的定义:

单位向量，单位向量可以用来表示方式，但单位向量的大小(模)为1

单位向量 = 向量 / 向量的模

这里简单说一下向量加法的概念：

A + B = C

几何解释是向量A通过向量B的平移得到向量C(A向量头连接B向量尾的向量)

接下来让我通过可视化绘制世界坐标系和可视化绘制两个Cube的连线来看看向量是如何表达出两个物体之间的方向和大小的。

/* * Description:             HandlesUtilities.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             HandlesUtilities.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEditor;
using UnityEngine;

/// <summary>
/// HandlesUtilities.cs
/// Handles辅助工具
/// </summary>
public static class HandlesUtilities
{
    /// <summary>
    /// 绘制有颜色的文本
    /// </summary>
    /// <param name="pos">坐标</param>
    /// <param name="text">文本</param>
    /// <param name="color">颜色</param>
    public static void DrawColorLable(Vector3 pos, string text, Color color)    {
    
        Color preColor = GUI.color;
        GUI.color = color;
        Handles.Label(pos, text);
        GUI.color = preColor;
    }
}

/* * Description:             VectorStudy.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorStudy.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;

/// <summary>
/// VectorStudy.cs
/// 向量学习
/// </summary>
public class VectorStudy : MonoBehaviour
{
    ******

    private void Start()    {
    
        var cube1ToCube2Vector = Cube2.transform.position - Cube1.transform.position;
        var cube2ToCube3Vector = Cube3.transform.position - Cube2.transform.position;
        var vectorAdd = cube1ToCube2Vector + cube2ToCube3Vector;
        TipTxt.text = $"红色表示Cube1,绿色表示Cube2,蓝色表示Cube3\n" +
                        $"Cube1世界坐标:{Cube1.transform.position.ToString()} 朝向:{Cube1.transform.forward.ToString()}\n" +
                        $"Cube2世界坐标系:{Cube2.transform.position.ToString()} 朝向:{Cube2.transform.forward.ToString()}\n" +
                        $"Cube3世界坐标系:{Cube3.transform.position.ToString()} 朝向:{Cube3.transform.forward.ToString()}\n" +
                        $"Cube1到Cube2的向量:{cube1ToCube2Vector.ToString()}\n" +
                        $"Cube1到Cube2的向量长度:{cube1ToCube2Vector.magnitude}\n"+
                        $"Cube2到Cube3的向量:{cube1ToCube2Vector.ToString()}\n" +
                        $"1->2 + 2->3 = {vectorAdd.ToString()}";
    }
}

/* * Description:             VectorStudyEditor.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorStudyEditor.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEditor;
using UnityEngine;

/// <summary>
/// VectorStudyEditor.cs
/// VectorStudy的Editor绘制
/// </summary>
[CustomEditor(typeof(VectorStudy))]
public class VectorStudyEditor : Editor
{
    /// <summary>
    /// Cube1属性
    /// </summary>
    SerializedProperty mCube1Property;

    /// <summary>
    /// Cube2属性
    /// </summary>
    SerializedProperty mCube2Property;

    /// <summary>
    /// Cube3属性
    /// </summary>
    SerializedProperty mCube3Property;

    /// <summary>
    /// 坐标系长度属性
    /// </summary>
    SerializedProperty mCoordinateSystemLengthProperty;

    /// <summary>
    /// Z轴颜色属性
    /// </summary>
    SerializedProperty mForwardAxisColorProperty;

    /// <summary>
    /// X轴颜色属性
    /// </summary>
    SerializedProperty mRightAxisColorProperty;

    /// <summary>
    /// Y轴颜色
    /// </summary>
    SerializedProperty mUpAxisColorProperty;

    /// <summary>
    /// 向量颜色
    /// </summary>
    SerializedProperty mVectorColorProperty;

    /// <summary>
    /// Cube1
    /// </summary>
    private GameObject mCube1;

    /// <summary>
    /// Cube2
    /// </summary>
    private GameObject mCube2;

    /// <summary>
    /// Cube3
    /// </summary>
    private GameObject mCube3;

    protected void OnEnable()    {
    
        mCube1Property = serializedObject.FindProperty("Cube1");
        mCube2Property = serializedObject.FindProperty("Cube2");
        mCube3Property = serializedObject.FindProperty("Cube3");
        mCoordinateSystemLengthProperty = serializedObject.FindProperty("CoordinateSystemLength");
        mForwardAxisColorProperty = serializedObject.FindProperty("ForwardAxisColor");
        mRightAxisColorProperty = serializedObject.FindProperty("RightAxisColor");
        mUpAxisColorProperty = serializedObject.FindProperty("UpAxisColor");
        mVectorColorProperty = serializedObject.FindProperty("VectorColor");
    }

    protected virtual void OnSceneGUI()    {
    
        InitData();
        DrawCubeInfo();
        DrawWorldCoordinateSystem();
        DrawVectorInfo();
    }

    /// <summary>
    /// 初始化数据
    /// </summary>
    private void InitData()    {
    
        mCube1 = mCube1Property?.objectReferenceValue != null ? mCube1Property.objectReferenceValue as GameObject : null;
        mCube2 = mCube2Property?.objectReferenceValue != null ? mCube2Property.objectReferenceValue as GameObject : null;
        mCube3 = mCube3Property?.objectReferenceValue != null ? mCube3Property.objectReferenceValue as GameObject : null;
    }

    /// <summary>
    /// 绘制Cube信息
    /// </summary>
    private void DrawCubeInfo()    {
    
        HandlesUtilities.DrawColorLable(mCube1.transform.position, "Cube1", Color.red);
        HandlesUtilities.DrawColorLable(mCube2.transform.position, "Cube2", Color.red);
        HandlesUtilities.DrawColorLable(mCube3.transform.position, "Cube3", Color.red);
    }

    /// <summary>
    /// 绘制世界坐标系
    /// </summary>
    private void DrawWorldCoordinateSystem()    {
    
        HandlesUtilities.DrawColorLable(Vector3.zero, "世界坐标系", Color.red);
        if (Event.current.type == EventType.Repaint)
        {
            Handles.color = mForwardAxisColorProperty.colorValue;
            Handles.ArrowHandleCap(1, Vector3.zero,
                                    Quaternion.LookRotation(Vector3.forward),
                                    mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);

            Handles.color = mRightAxisColorProperty.colorValue;
            Handles.ArrowHandleCap(1, Vector3.zero,
                                    Quaternion.LookRotation(Vector3.right),
                                    mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);

            Handles.color = mUpAxisColorProperty.colorValue;
            Handles.ArrowHandleCap(1, Vector3.zero,
                                    Quaternion.LookRotation(Vector3.up),
                                    mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);
        }
    }

    /// <summary>
    /// 绘制相关向量
    /// </summary>
    private void DrawVectorInfo()    {
    
        if (Event.current.type == EventType.Repaint)
        {
            if (mCube1 != null && mCube2 != null && mCube3 != null)
            {
                var cube1ToCube2Vector = mCube2.transform.position - mCube1.transform.position;
                var cube2ToCube3Vector = mCube3.transform.position - mCube2.transform.position;
                var vectorAdd = cube1ToCube2Vector + cube2ToCube3Vector;
                Handles.color = mVectorColorProperty.colorValue;
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(cube1ToCube2Vector),
                                        cube1ToCube2Vector.magnitude, EventType.Repaint);
                Handles.ArrowHandleCap(1, mCube2.transform.position,
                                        Quaternion.LookRotation(cube2ToCube3Vector),
                                        cube2ToCube3Vector.magnitude, EventType.Repaint);
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(vectorAdd),
                                        vectorAdd.magnitude, EventType.Repaint);
                Handles.Label(mCube1.transform.position + cube1ToCube2Vector / 2, "1->2");
                Handles.Label(mCube2.transform.position + cube2ToCube3Vector / 2, "2->3");
                Handles.Label(mCube1.transform.position + vectorAdd / 2, "1->2 + 2->3");
            }
        }
    }
}

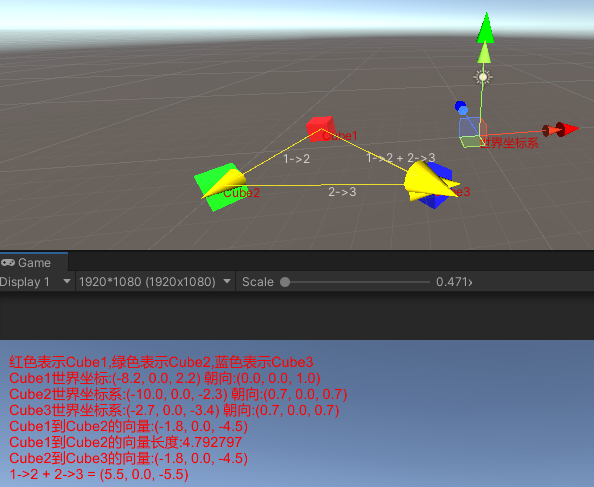
通过Handles相关接口，我们成功绘制出了以下东西:

1. 世界坐标系
2. Cube1到Cube2的向量
3. Cube2到Cube3的向量
4. 1->2 + 2->3的向量

可以看到Cube2坐标-Cube1坐标=从Cube1位置指向Cube2位置的向量，也就是说B - A = A->B

同时上面的可视化也显示了，A->B + B->C = A->C的向量加法规则，减法反向理解即可。

接下来我们要学习了解向量里比较重要的两个运算概念:

1. 点乘
2. 叉乘

Note:

1. 方向并不完全和方位相同
2. 数学中专门研究向量的分支称作线性代数
3. 向量加法满足交换律，但向量减法不满足交换律。因为得到的向量方向相反。

点乘

点乘(也称为内积)，记做a.b

a.b = a1 b1 + a2 b2 + a3 b3 … + an bn

几何解释:

点乘等于向量大小与向量夹角的cosθ值的积。点乘结果描述了两个向量的”相似”程度，点乘结果越大，两向量越相近。

a.b = |a| |b| cosθ

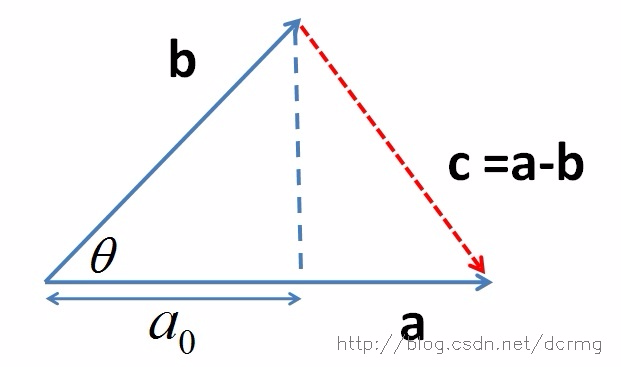
根据上面的公式和图我们可以看出，点乘在几何里的可以理解成a向量在b向量上的投影乘以b向量的模

通过上面的公式我们反向推到夹角的计算公式如下:

θ = arccor(a.b / |a| * |b|)

如果我们不关心点乘的大小，那么从点乘的值我们可以判定两个向量之间的夹角情况:

1. a.b > 0 —> 方向基本相同，夹角在0到90度之间
2. a.b = 0 —> 正交，两向量垂直
3. a.b < 0 —> 方向基本相反，夹角在90-180度之间

接下来让我们通过Unity实战可视化辅助我们学习向量点乘:

/* * Description:             VectorStudyEditor.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorStudyEditor.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEditor;
using UnityEngine;

/// <summary>
/// VectorStudyEditor.cs
/// VectorStudy的Editor绘制
/// </summary>
[CustomEditor(typeof(VectorDotStudy))]
public class VectorDotStudyEditor : Editor
{
    ******


    /// <summary>
    /// 绘制相关向量
    /// </summary>
    private void DrawVectorInfo()    {
    
        if (Event.current.type == EventType.Repaint)
        {
            if (mCube1 != null && mCube2 != null && mCube3 != null)
            {
                var cube1ToCube2Vector = mCube2.transform.position - mCube1.transform.position;
                var cube1ToCube3Vector = mCube3.transform.position - mCube1.transform.position;
                var vectorDot = Vector3.Dot(cube1ToCube2Vector, cube1ToCube3Vector);
                var radians = Mathf.Acos(vectorDot / (cube1ToCube2Vector.magnitude * cube1ToCube3Vector.magnitude));
                var angle = Mathf.Rad2Deg * radians;
                Handles.color = mVectorColorProperty.colorValue;
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(cube1ToCube2Vector),
                                        cube1ToCube2Vector.magnitude, EventType.Repaint);
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(cube1ToCube3Vector),
                                        cube1ToCube3Vector.magnitude, EventType.Repaint);
                Handles.Label(mCube1.transform.position + cube1ToCube2Vector / 2, "1->2");
                Handles.Label(mCube1.transform.position + cube1ToCube3Vector / 2, "1->3");
                HandlesUtilities.DrawColorLable(mCube1.transform.position, $"夹角:{angle}", Color.green);
            }
        }
    }
}

/* * Description:             VectorDotStudy.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorDotStudy.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;

/// <summary>
/// VectorDotStudy.cs
/// 向量点乘学习
/// </summary>
public class VectorDotStudy : MonoBehaviour
{
    ******

    private void Start()    {
    
        var cube1ToCube2Vector = Cube2.transform.position - Cube1.transform.position;
        var cube1ToCube3Vector = Cube3.transform.position - Cube1.transform.position;
        var vectorDot = Vector3.Dot(cube1ToCube2Vector, cube1ToCube3Vector);
        var radians = Mathf.Acos(vectorDot / (cube1ToCube2Vector.magnitude * cube1ToCube3Vector.magnitude));
        var angle = Mathf.Rad2Deg * radians;
        TipTxt.text = $"红色表示Cube1,绿色表示Cube2,蓝色表示Cube3\n" +
                        $"Cube1世界坐标:{Cube1.transform.position.ToString()} 朝向:{Cube1.transform.forward.ToString()}\n" +
                        $"Cube2世界坐标系:{Cube2.transform.position.ToString()} 朝向:{Cube2.transform.forward.ToString()}\n" +
                        $"Cube3世界坐标系:{Cube3.transform.position.ToString()} 朝向:{Cube3.transform.forward.ToString()}\n" +
                        $"Cube1到Cube2的向量:{cube1ToCube2Vector.ToString()}\n" +
                        $"Cube1到Cube3的向量:{cube1ToCube3Vector.magnitude}\n" +
                        $"1->2 点乘 2->3 = {vectorDot}\n" +
                        $"1->2和2->3的夹角:{angle}";
    }
}

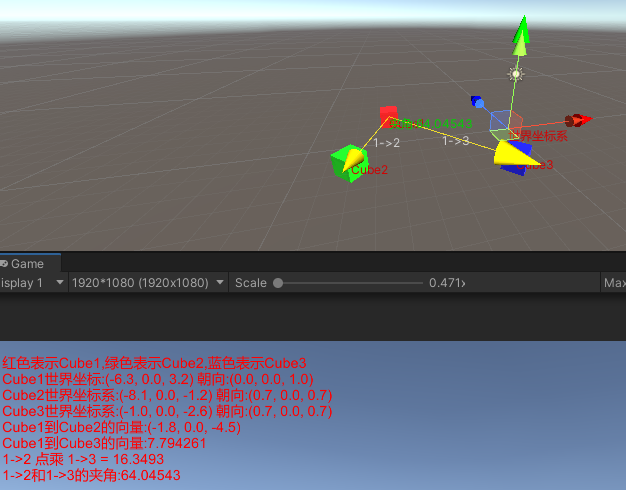
通过上面的计算和可视化，可以看到我们通过Mathf.Acos(a.b / (|a| |b|)) Mathf.Rad2Deg实现了点乘角度的逆推。

并且因为点乘是a.b = |a| |b| cos(θ)，所以从点乘的结果我们可以分析出两个向量的角度情况:

a.b > 0表示a和b向量夹角为0度到90度

a.b==0表示a和b向量垂直

a.b<0表示a和b向量夹角为90度到180度

Note:

1. 点乘满足交换律
2. 点乘对零向量的解释是，零向量和任意其他向量垂直
3. Unity Mathf.Acos()返回的是弧度而非角度，需要通过乘以Mathf.Rad2Deg进行角度转换

叉乘

叉乘又称叉积，和点乘不一样，点乘得到一个标量并满足交换律，向量叉乘得到一个向量并且不满足交换律

​ [x1] [x2] [y1 z2 - z1 * y1 ]

​ a X b = [y1] [y2] = [ z1 x2 - x1 * z2 ]

​ [z1] [y3] [ x1 y2 - y1 * x2 ]

几何解释：

叉乘得到的向量垂直于原来的两个向量

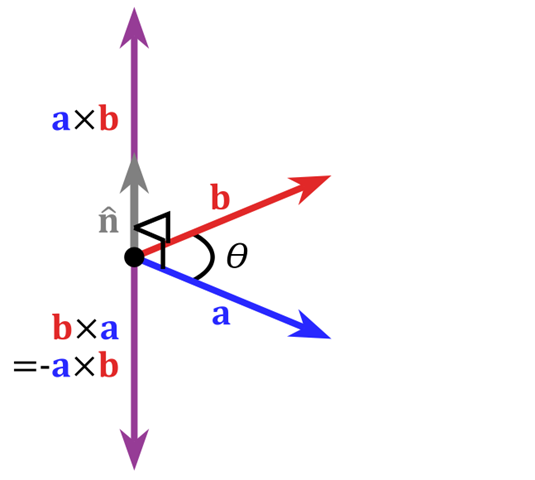
|aXb|=|a||b|sinθ

从2维平面几何来说，a向量和b向量的叉乘长度等于以a向量和b向量为边的平行四边形面积。

我们知道了a向量叉乘b向量得到的是一个垂直于a和b平面的向量，那么这个向量是朝上还是朝下是如何决定的了？

通过把a向量和b向量首尾相连，在左手坐标系里如果a和b成顺时针，那么aXb的结果向量向外，反之向里。右手坐标系中则恰好相反。

接下来让我们结合实战，看下我们是如何利用叉乘计算出垂直a和b向量的c向量的:

/* * Description:             VectorCrossStudyEditor.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorCrossStudyEditor.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEditor;
using UnityEngine;

/// <summary>
/// VectorCrossStudyEditor.cs
/// VectorCrossStudy的Editor绘制
/// </summary>
[CustomEditor(typeof(VectorCrossStudy))]
public class VectorCrossStudyEditor : Editor
{
    ******

    /// <summary>
    /// 绘制相关向量
    /// </summary>
    private void DrawVectorInfo()    {
    
        if (Event.current.type == EventType.Repaint)
        {
            if (mCube1 != null && mCube2 != null && mCube3 != null)
            {
                var cube1Forward = mCube1.transform.forward;
                var cube1ToCube2 = mCube2.transform.position - mCube1.transform.position;
                var vectorDot = Vector3.Dot(cube1Forward, cube1ToCube2);
                var radians = Mathf.Acos(vectorDot / (cube1Forward.magnitude * cube1ToCube2.magnitude));
                var angle = Mathf.Rad2Deg * radians;
                var vectorCross = Vector3.Cross(cube1Forward, cube1ToCube2);
                vectorCross = (angle <= Mathf.Epsilon && angle >= -Mathf.Epsilon) ? cube1Forward : vectorCross;
                Handles.color = mVectorColorProperty.colorValue;
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(cube1Forward),
                                        mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(cube1ToCube2),
                                        mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(vectorCross),
                                        mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);
                HandlesUtilities.DrawColorLable(mCube1.transform.position, $"夹角:{angle}", Color.green);
            }
        }
    }
}

/* * Description:             VectorCrossStudy.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorCrossStudy.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;

/// <summary>
/// VectorCrossStudy.cs
/// 向量叉乘学习
/// </summary>
public class VectorCrossStudy : MonoBehaviour
{
    ******

    /// <summary>
    /// 旋转角度
    /// </summary>
    private float mAngle;

    /// <summary>
    /// 旋转轴
    /// </summary>
    private Vector3 mRotateAxis;

    private void Start()    {
    
        RotateBtn.onClick.AddListener(OnRotateBtnClick);
        var cube1Forward = Cube1.transform.forward;
        var cube1ToCube2 = Cube2.transform.position - Cube1.transform.position;
        var vectorDot = Vector3.Dot(cube1Forward, cube1ToCube2);
        var radians = Mathf.Acos(vectorDot / (cube1Forward.magnitude * cube1ToCube2.magnitude));
        mAngle = Mathf.Rad2Deg * radians;
        mRotateAxis = Vector3.Cross(cube1Forward, cube1ToCube2);
        var rotationDirection = mRotateAxis.y > 0 ? "顺时针" : "逆时针";
        TipTxt.text = $"红色表示Cube1,绿色表示Cube2\n" +
                        $"Cube1世界坐标:{Cube1.transform.position.ToString()} 朝向:{Cube1.transform.forward.ToString()}\n" +
                        $"Cube2世界坐标系:{Cube2.transform.position.ToString()} 朝向:{Cube2.transform.forward.ToString()}\n" +
                        $"Cube1朝向:{cube1Forward.ToString()}\n" +
                        $"Cube1到Cube2向量:{cube1ToCube2.ToString()}\n" +
                        $"Cube1朝向 点乘 Cube1到Cube2向量 = {vectorDot}\n" +
                        $"Cube1朝向 叉乘 Cube1到Cube2向量 = {mRotateAxis.ToString()}\n" +
                        $"Cube1看向Cube2旋转方向:{rotationDirection}\n" +
                        $"Cube1看向Cube2旋转角度:{mAngle}";
    }

    /// <summary>
    /// 点击旋转Cube1看向Cube2
    /// </summary>
    public void OnRotateBtnClick()    {
    
        Cube1.transform.Rotate(mRotateAxis, mAngle);
        Debug.Log($"Cube1看向Cube2旋转方向:{mRotateAxis} 旋转角度:{mAngle}");
    }
}

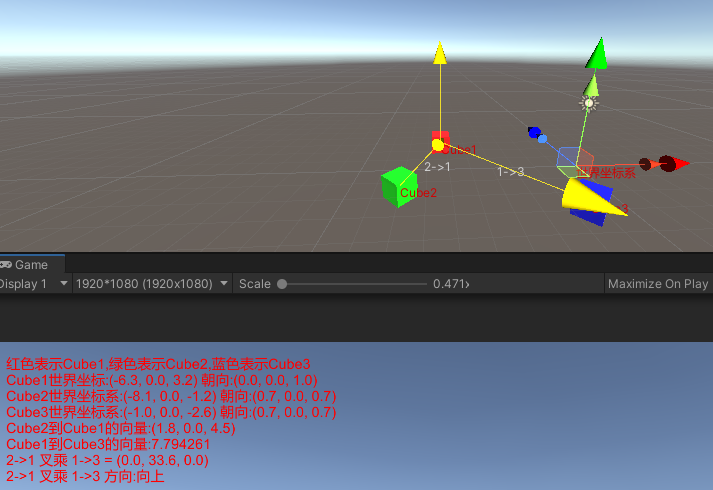
从上面的绘制可以看出，向量2-1叉乘向量1-3的结果是(0, 33.6, 0)，即结果向量是向上的，这和Unity左手坐标系，a和b头尾相连顺时针则向外(即向上)是符合的。

Note:

1. 点乘和叉乘一起时，叉乘优先计算
2. 叉乘不满足交换律和结合律
3. 判定叉乘A叉乘B方向时可以通过四指指向A向量，然后转向B向量，此时大拇指的方向就是叉乘向量方向

运用

点乘和叉乘最典型的运用就是通过点乘计算两个向量的夹角，通过叉乘计算两个向量的角度方向。

典型的问题就是已知玩家A和B的位置和朝向，如何让玩家A看向玩家B。

要解决上述问题，我们需要通过玩家A到玩家B位置的向量和玩家A的朝向向量来计算出他们的夹角和旋转方向。

接下来结合Unity实战，让我们看看，我们是如何通过点乘和叉乘计算出两个向量的旋转角度和方向的:

/* * Description:             VectorUsingStudyEditor.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorUsingStudyEditor.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEditor;
using UnityEngine;

/// <summary>
/// VectorUsingStudyEditor.cs
/// VectorUsingStudy的Editor绘制
/// </summary>
[CustomEditor(typeof(VectorUsingStudy))]
public class VectorUsingStudyEditor : Editor
{
    ******

    /// <summary>
    /// 绘制相关向量
    /// </summary>
    private void DrawVectorInfo()    {
    
        if (Event.current.type == EventType.Repaint)
        {
            if (mCube1 != null && mCube2 != null && mCube3 != null)
            {
                var cube1Forward = mCube1.transform.forward;
                var cube1ToCube2 = mCube2.transform.position - mCube1.transform.position;
                var vectorDot = Vector3.Dot(cube1Forward, cube1ToCube2);
                var radians = Mathf.Acos(vectorDot / (cube1Forward.magnitude * cube1ToCube2.magnitude));
                var angle = Mathf.Rad2Deg * radians;
                var vectorCross = Vector3.Cross(cube1Forward, cube1ToCube2);
                vectorCross = (angle <= Mathf.Epsilon && angle >= -Mathf.Epsilon) ? cube1Forward : vectorCross;
                Handles.color = mVectorColorProperty.colorValue;
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(cube1Forward),
                                        mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(cube1ToCube2),
                                        mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);
                Handles.ArrowHandleCap(1, mCube1.transform.position,
                                        Quaternion.LookRotation(vectorCross),
                                        mCoordinateSystemLengthProperty.floatValue, EventType.Repaint);
                HandlesUtilities.DrawColorLable(mCube1.transform.position, $"夹角:{angle}", Color.green);
            }
        }
    }
}

/* * Description:             VectorUsingStudy.cs * Author:                  TONYTANG * Create Date:             2022/03/17 */
 * Description:             VectorUsingStudy.cs
 * Author:                  TONYTANG
 * Create Date:             2022/03/17
 */

using System.Collections;
using System.Collections.Generic;
using UnityEngine;
using UnityEngine.UI;

/// <summary>
/// VectorUsingStudy.cs
/// 向量点乘和叉乘实战学习
/// </summary>
public class VectorUsingStudy : MonoBehaviour
{
    ******
    
    /// <summary>
    /// 旋转角度
    /// </summary>
    private float mAngle;

    /// <summary>
    /// 旋转轴
    /// </summary>
    private Vector3 mRotateAxis;

    private void Start()    {
    
        RotateBtn.onClick.AddListener(OnRotateBtnClick);
        var cube1Forward = Cube1.transform.forward;
        var cube1ToCube2 = Cube2.transform.position - Cube1.transform.position;
        var vectorDot = Vector3.Dot(cube1Forward, cube1ToCube2);
        var radians = Mathf.Acos(vectorDot / (cube1Forward.magnitude * cube1ToCube2.magnitude));
        mAngle = Mathf.Rad2Deg * radians;
        mRotateAxis = Vector3.Cross(cube1Forward, cube1ToCube2);
        var rotationDirection = mRotateAxis.y > 0 ? "顺时针" : "逆时针";
        TipTxt.text = $"红色表示Cube1,绿色表示Cube2\n" +
                        $"Cube1世界坐标:{Cube1.transform.position.ToString()} 朝向:{Cube1.transform.forward.ToString()}\n" +
                        $"Cube2世界坐标系:{Cube2.transform.position.ToString()} 朝向:{Cube2.transform.forward.ToString()}\n" +
                        $"Cube1朝向:{cube1Forward.ToString()}\n" +
                        $"Cube1到Cube2向量:{cube1ToCube2.ToString()}\n" +
                        $"Cube1朝向 点乘 Cube1到Cube2向量 = {vectorDot}\n" +
                        $"Cube1朝向 叉乘 Cube1到Cube2向量 = {mRotateAxis.ToString()}\n" +
                        $"Cube1看向Cube2旋转方向:{rotationDirection}\n" +
                        $"Cube1看向Cube2旋转角度:{mAngle}";
    }

    /// <summary>
    /// 点击旋转Cube1看向Cube2
    /// </summary>
    public void OnRotateBtnClick()    {
    
        Cube1.transform.Rotate(mRotateAxis, mAngle);
        Debug.Log($"Cube1看向Cube2旋转方向:{mRotateAxis} 旋转角度:{mAngle}");
    }
}

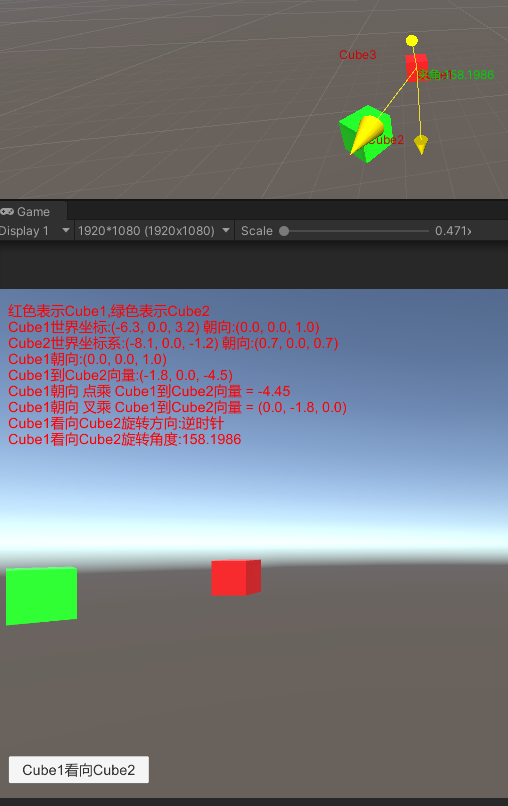
从上面的效果图可以看出，当Cube2在不同的位置时，我们通过点乘和叉乘成功算出了Cube1朝向向量到Cube1到Cube2位置向量的旋转角度和选择方向。

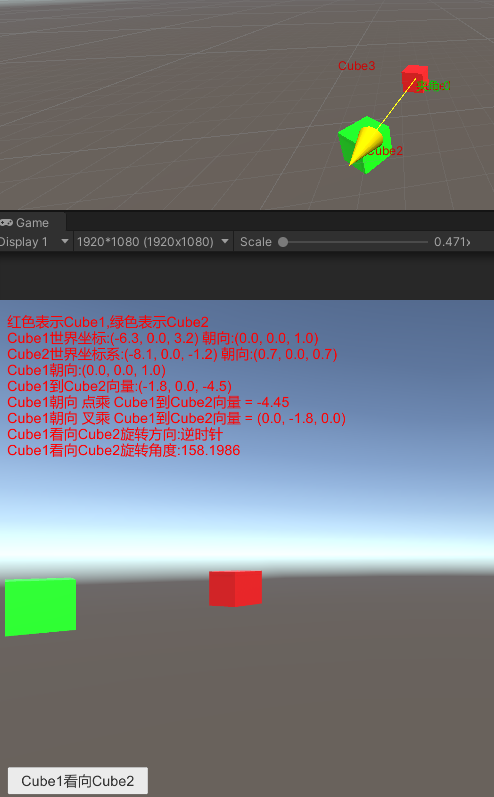
通过点击Cube1看向Cube2，我们调用transform.Rotate(叉乘的向量, 点乘逆推的角度)我们可以看到，Cube1实现通过绕(0, -1.8, 0)选择158度实现了看向Cube2。

如果只是单纯的让玩家B看向玩家A，实战中我们并不会向上面一样根据公式的逆推实现旋转轴和旋转角度，而是直接使用Unity提供的API，比如transform.LookAt(玩家ATransform)即可实现玩家B看向玩家A的需求。但了解底层的实现原理以及叉乘点乘的实际用处还是很有必要的。

上面有一个细节要注意的是，Quaternion.LookRotation()不支持看向一个零向量，所以通过判定点旋转角度是否为0来判定是否Cube1朝向和Cube1连接Cube2的向量方向一致

更多关于向量的运算参考Vector3相关的接口使用，在后续实战中更多的学习运用，这里就不一一提及了。

Note:

1. |aXb|为0表示两个向量平行
2. 利用叉乘结果y大于0还是y小于0区分方向的同时，我们还能用于推断向量A在向量B的左侧还是右侧(大前提是两个向量在XZ平面)
3. 想判定两个向量的前后关系，可以用点乘的正负结果来判定

矩阵

待添加……

欧拉角与四元数

待添加……

几何检测

待添加……

可见性检测

待添加……

数学概念

待添加……

学习总结

待添加……

Github

个人Github:

MathStudy

详细的Editor绘制学习参考:

UnityEditor知识

Reference

计算机图形学 5：齐次坐标与 MVP 矩阵变换

向量内积（点乘）和外积（叉乘）概念及几何意义